こんにちはロウシです。
いつも記事を一読してもらってありがとうございます。
今回は微積を使ってきちんと高校物理を理解する」シリーズの第一回「座標系 速度 加速度 編」です。
この記事を読めば、位置の関数から速度、加速度を求める事ができるようになります。
この記事では高校数学レベルの三角関数、ベクトルは理解しているものとします。
重要な事だけ知りたい方は目次からまとめにいってください。
この記事でわかることはこういったことです。
- 物理での位置の表し方
- 速度の定義
- 加速度の定義
力学の目的

今回から力学を学んでいくわけですが、そもそも力学の最終目標はなんでしょうか。
それは物体がどのように運動していつどこにあるのかを予言(知る)ことです。
そのために我々は数学という名の言語を用います。
日常の言語では自然を記述することが難しいからです。
数学は言語であると考えた方が物理の理解はしやすいと思います。
つまり数式は物理現象を表現しているものなのです。
下準備 ベクトルの表記法

高校数学では\(a\)がベクトルであることを示すとき\(\vec{a}\)の用に上に矢印を描いていましたが大学以降の数学や物理では\(\boldsymbol{a}\)の用に太字でベクトルであることを表します。
つまり、ある量\(a\)がベクトルであることを\(\boldsymbol{a}\)のようにあらわします。
手書きでノートに書く場合ベクトルは二重線で表現します。
手書きの仕方について詳しくは各自ネットで調べてみてください。
物理での位置の表し方

「力学の目的」でも話しましたが、力学は物体の運動を予言することが目標です。
そのためにはまず位置を数式で定義しないといけません。
物理学では物体の位置を「位置ベクトル」で定義します。
なぜ通常の座標で定義しないのか。
それは物体の運動を扱うときに向きと大きさの両方を扱うからです。
ベクトルは向きと大きさを持った量なので物体の運動を扱うときにぴったりなのです。
ここでは2次元での話を扱います。3次元も2次元と同様に考えることができます。
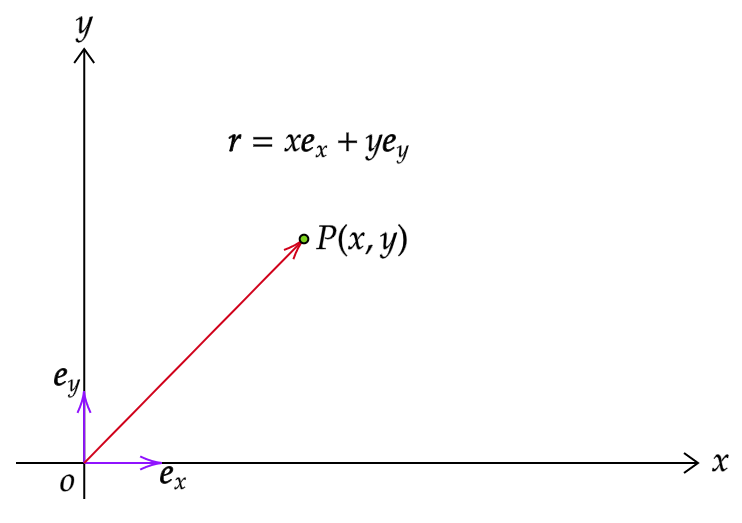
二次元空間内にある点\(P\)の位置ベクトルを\(\boldsymbol{r}\)とします。点\(P\)の座標が二次元直交座標系(普段高校数学などで使われる座標系)で(\(x\),\(y\))で与えられているとします。
二次元直交座標系の各軸の単位ベクトル(大きさが1のベクトル)\(\boldsymbol{e_x}\),\(\boldsymbol{e_y}\)を
$$\boldsymbol{e_x}=(1,0)$$
$$\boldsymbol{e_y}=(0,1)$$
とすると位置\(\boldsymbol{r}\)は次のように表すことができます。
$$\boldsymbol{r}=(x,y)=x\boldsymbol{e_x}+y\boldsymbol{e_y}$$
先程言ったように、 力学の目標は\(\boldsymbol{r}(t)\)を完全に理解することです。
\(\boldsymbol{r}(t)\)は\(\boldsymbol{r}\)が時刻\(t\)の関数であることを表しています。
以下の議論では\(\boldsymbol{r}(t)\)が与えられたものとして議論を進めます。
速度の定義

二次元での一般的な速度の話に入る前に速度と速さの違いをはっきりさせておきます。
速さは速度の絶対値の事です。
つまり速度は\(-\)の値をとりえます。
一次元で考えると右を\(+\)とすると左が\(-\)になります。
一次元で\(-\)の速度を持つと言うことは左に物体が進んでいくということです。
つぎの節は簡単のため\(\boldsymbol{r}(t)=(x(t),0)\)から考えます。
関数\(x(t)\)は時刻\(t\)の関数で物体の\(x\)方向の位置を表します。
\(x(t_1)\)は時刻\(t_1\)での物体の\(x\)軸での位置を表します。
一次元の場合
一次元での物体の変位
ある時刻\(t=t_1\)に位置\(x(t_1)\)にいた点\(Q\)が\(t=t_2\)(\(>t_1\))に位置\(x(t_2)\)に移動したとします。
この状況で時刻\(t_1\sim t_2\)の位置の変化量
$$\Delta x =x(t_2)-x(t_1)$$
を変位と言います。
ここで用いた\(\Delta \)は「幅」や「差分」を表す記号です。
\(\Delta t\)と描くことで\(t\)という量の差を表します。
また\(\Delta x\)は\(\Delta ×x\)ではなく、 \(\Delta x\)という感じで一つのセットです。
一次元での物体の平均の速度
ある時刻\(t=t_1\)に位置\(x(t_1)\),\(t=t_2\)(\(>t_1\))に位置\(x(t_2)\)にいた点\(Q\)の平均の速度は変位を変位にかかった時間で割った、
$$\bar{v} \unicode{x225D} \displaystyle \frac{x(t_2)-x(t_1)}{t_2-t_1}$$
で定義されます。
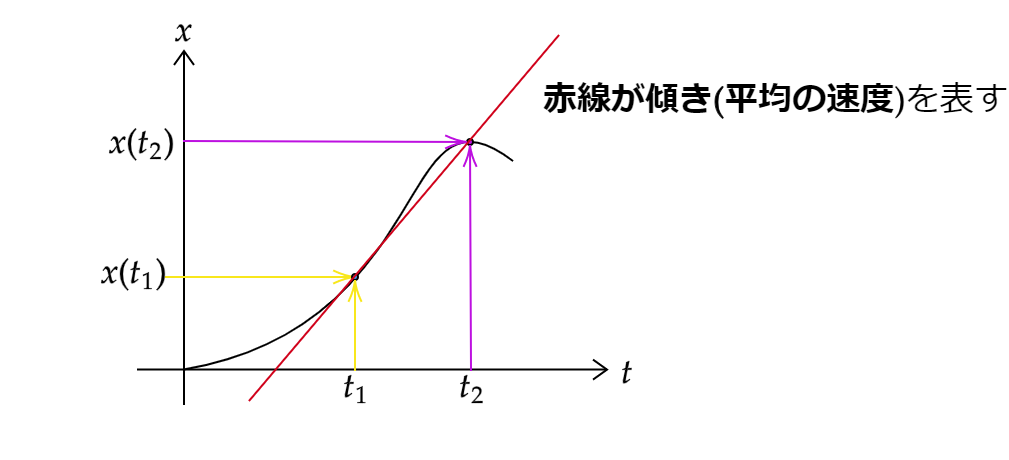
これは小学生でならう速さとほとんど同じ定義です。
ですが速度ですので\(-\)の値をとりえます(その場合\(x\)軸方向の反対方向に進んでいきます)。
一次元での物体の速度
平均の速度は二つの位置とその間を移動するのにかかる時間がわかれば計算することができました。
しかし平均の速度というだけあって、途中で速度がどのように変化したのかはわかりません。例えば下記のグラフだと
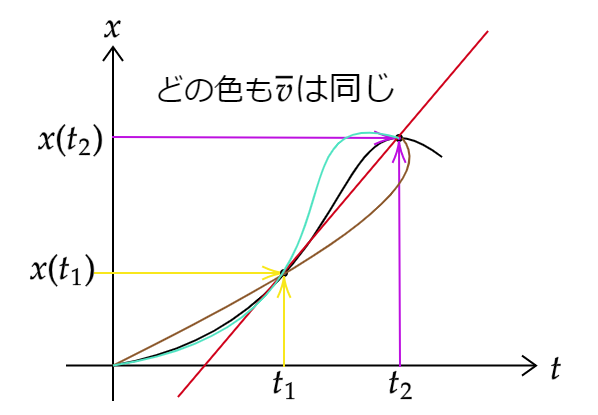
平均の速度では上のグラフのように始点と終点と所要時間が同じならばその間にどんな変化をしようと速度に影響しません。
これは物体の位置や速度を正確に知りたい我々にとってはよくないです。
そこで\(t_1\sim t_2\)の時間
$$\Delta t =t_2-t_1$$
において\(t_2\)を限りなく\(t_1\)に近づける(\(\Delta t\)を限りなく\(0\)に近づけるつまり\( \lim_{\Delta t\to 0}\))を先程の平均の速度の式に行って、
$$v(t_1)=\displaystyle \lim_{ t_2 \to t_1 } \frac{ x(t_2) – x(t_1) }{ t_2-t_1 }= \lim_{ \Delta t \to 0 } \frac{ x(t_1+\Delta t) – x(t_1) }{ \Delta t }$$
を時刻\(t_1\)における瞬間の速度あるいは速度と呼びます。これは\(x-t\)グラフ上での\(x(t)\)の\(x(t_1)\)での傾きを表しています。
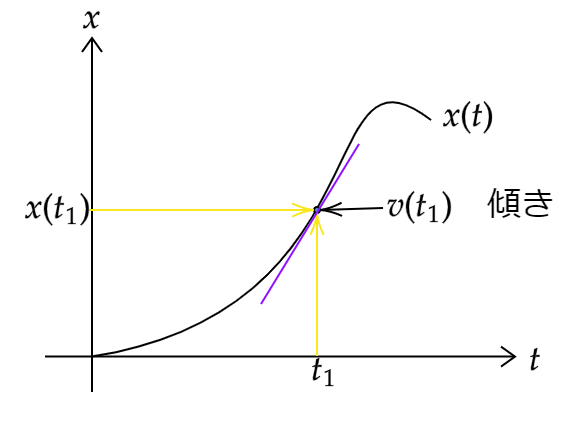
ところでこの形の式どこかで見たことありませんか。
そうです。この形は\(x\)を変数とする関数\(f(x)\)の\(x_1\)における微分係数の定義式
$$f'(x_1)=\displaystyle \lim_{ \Delta x \to 0 } \frac{ f(x_1 + \Delta x) – f(x_1) }{ \Delta x }\tag{1}$$
と全く同じ形をしています。
よって時刻\(t_1\)における\(v(t_1)\)は位置\(x(t)\)の時刻\(t_1\)における微分係数で定義されていることが分かります。
速度自体の関数を知りたければ\((1)\)の\(t_1\)を\(t\)に読み替えます。
つまり位置\(x(t)\)の導関数を計算します。よって速度は位置\(x(t)\)の微分をすることで求める事ができます。
式にすると、
$$v(t)=\dot{x}=\displaystyle \frac{dx(t)}{dt}=\lim_{ \Delta t \to 0 } \frac{ x(t + \Delta t) – x(t) }{ \Delta t }$$
となります。ここで\(\displaystyle \frac{dx(t)}{dt}\)は\(x(t)\)を\(t\)で微分した事を表し、\(\dot{x}\)は\(x(t)\)を一回時間微分した事を表します。
物理では何を何で微分したのかが重要ですのでよく\(\displaystyle \frac{dx(t)}{dt}\)や\(\dot{x}\)のように描きます。
物理では何か(関数)を時間微分したとき文字の上に・を描きます。・一回につき一回時間微分を表します。例、\(\dot{x}\)、\(\ddot{x}\)、\(\dot{v}\)など。
\(\displaystyle \frac{dx(t)}{dt}\)は決して分数ではないので勘違いしないようにしてください。
二次元以上の場合

二次元以上の場合も先程と同様にかんがえることができます。
つまり、二次元空間内なら\(x\)軸方向と\(y\)軸方向の運動に分けて考えれば先程と同様にできます。
二次元空間内にある点\(Q\)の時刻\(t\)における位置が二次元直交座標で\(\boldsymbol{r}=(x,y)\)とします。
時刻\(t_1\sim t_2\)間の変位\(\Delta \boldsymbol{r}\)は
$$\Delta \boldsymbol{r}=\boldsymbol{r}(t_2)-\boldsymbol{r}(t_1)=((x(t_2)-x(t_1)),(y(t_2)-y(t_1)))$$
です。よって時刻\(t_1\)の速度は、
$$\boldsymbol{v}(t_1)=\displaystyle \lim_{ \Delta t \to 0 } \frac{ \boldsymbol{r}(t_1+\Delta t) – \boldsymbol{r}(t_1) }{ \Delta t }$$
となります。よって\(\boldsymbol{v}(t)\)は、
$$\boldsymbol{v}(t)=\displaystyle \frac{d\boldsymbol{r}}{dt}=\left(\frac{dx}{dt},\frac{dy}{dt}\right)$$
となります。二次元空間や三次元空間でも各座標軸成分ごとに速度を求めれば、全体の速度も求めることができます。
速度が微分で表せるわけ

なぜ速度を微分で表すことができるのでしょうか。
速度を言葉で表すと、
「速度とは位置の時間変化率」です。
位置が時間でどのように変化するかを視覚的に見れるようにしたのが\(x-t\)(縦軸に位置、横軸に時間をとったグラフ)グラフです。
そして位置が時間でどのような変化を追っていくかつまり\(x-t\)グラフの傾きを求めることによって速度を求める事ができます。
微分係数はある瞬間でのグラフの傾きを表していました。
だから速度は位置(正確には関数)を微分することによって得ることができます。
なので\(x-t\)グラフ上でのある一点での傾きを求める(速度を求める)は微分係数を求める事と同じなのです。
この考え方は加速度でも同様です。
加速度の定義

加速度は速度の概念の発展系ですので、さきほどの議論が理解できていればすんなりと理解できると思います。
ですのですこし議論が駆け足になるかもしれません。
加速度は後々わかるようにニュートンの運動の法則におけるすごく重要な物理量ですのでしっかり理解していってください。
具体的な話に入る前に加速度とは何かをお話します。
加速度とは一言で言うと、「速度の時間変化率」です。
つまりある時刻で速度がどのように変化するかを表すものです。
そして数学的な構造は先程の速度と変わりません。
イメージ的には「速度の速度」といったところです。
一次元の場合
一次元での平均の加速度
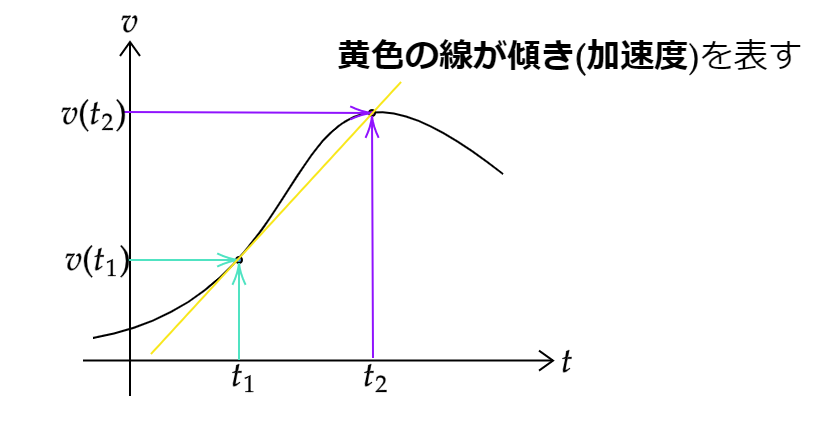
ある時刻\(t=t_1\)に速度\(v(t_1)\),\(t=t_2\)(\(>t_1\))に速度\(v(t_2)\)を持っていた点\(Q\)の平均の加速度は平均の速度を速度が変わるのにかかった時間で割った、
$$\bar{a} \unicode{x225D} \displaystyle \frac{v(t_2)-v(t_1)}{t_2-t_1}$$
で定義されます。
一次元での物体の加速度
速度の場合と同様に瞬間の加速度(あるいは加速度)を考えます。
先程ある物体\(Q\)の時刻\(t_1\)における速度は位置\(x(t)\)をもちいて、
$$v(t_1)=\lim_{ \Delta t \to 0 } \frac{ x(t_1+\Delta t) – x(t_1) }{ \Delta t }$$
で表され、\(x(t)\)の時刻\(t_1\)での微分係数に等しい事を知りました。
これと同様に考えてある物体\(Q\)の時刻\(t_1\)における加速度は速度\(v(t)\)をもちいて、
$$a(t_1) \unicode{x225D} \lim_{ \Delta t \to 0 } \frac{ v(t_1+\Delta t) – v(t_1) }{ \Delta t }$$
で定義されます。そして加速度の関数は\(t_1\)を\(t\)に読み替えて、速度を時間微分した関数(導関数)
$$a(t) \unicode{x225D} \displaystyle \frac{dv(t)}{dt}=\lim_{ \Delta t \to 0 } \frac{ v(t + \Delta t) – v(t) }{ \Delta t }$$
で定義されます。これは速度と同様に\(v-t\)グラフ上での\(v(t)\)の傾きを表しています。
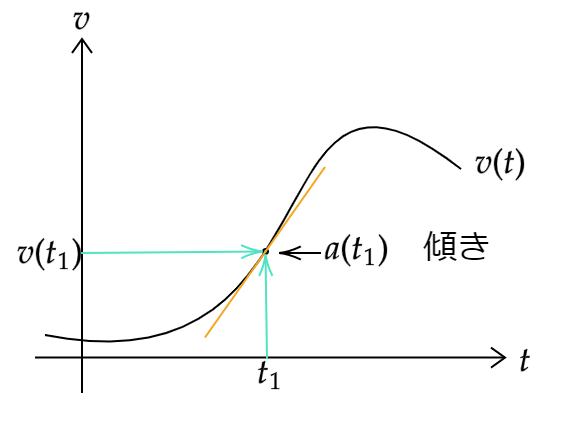
また加速度は、
$$a(t)=\dot{v}=\ddot{x}= \displaystyle \frac{dv(t)}{dt}=\frac{d^2x(t)}{dt^2}$$
のように書き換えることもできます。つまり加速度は位置\(x(t)\)の二回微分で求める事ができます。
二次元以上の場合

二次元以上の加速度も速度の時と同様に考えることができます。
二次元空間内にある点\(Q\)の時刻\(t\)における速度を\(\boldsymbol{v}(t)=(v_x,v_y)\)とすると時刻\(t_1\)における加速度は、
$$\boldsymbol{a}(t_1)=\displaystyle \lim_{ \Delta t \to 0 } \frac{ \boldsymbol{v}(t_1+\Delta t) – \boldsymbol{v}(t_1) }{ \Delta t }$$
で表されます。\(t_1\)を\(t\)に読み替えると、
$$\boldsymbol{a}(t)=\displaystyle \frac{d\boldsymbol{v}}{dt}=\left(\frac{dv_x}{dt},\frac{dv_y}{dt}\right)=\frac{d^2\boldsymbol{r}}{dt^2}=\left(\frac{d^2x}{dt^2},\frac{d^2y}{dt^2}\right)$$
になり二次元空間内での加速度を導くことができます。
まとめ
- 速度は位置の時間変化率なので二次元直交座標の場合$$\boldsymbol{v}(t)=\displaystyle \frac{d\boldsymbol{r}}{dt}=\left(\frac{dx}{dt},\frac{dy}{dt}\right)$$で表される
- 加速度は速度の時間変化率なので二次元直交座標の場合$$\boldsymbol{a}(t)=\displaystyle \frac{d\boldsymbol{v}}{dt}=\left(\frac{dv_x}{dt},\frac{dv_y}{dt}\right)=\frac{d^2\boldsymbol{r}}{dt^2}=\left(\frac{d^2x}{dt^2},\frac{d^2y}{dt^2}\right)$$で表される
今回グラフを作るのにつかったサイトは
↓
https://www.mathcha.io/
下に書いてある本は物理を最初学ぶのにぴったりの本なので興味があったらぜひ読んでください。


