【解説】微分方程式で単振動の運動方程式を解く！

こんにちはロウシです。

いつも記事を一読してもらってありがとうございます。

今回の記事は「単振動の運動方程式」の解き方を解説しようと思います。

単振動の運動方程式とはこのような式です。

$$m\displaystyle \frac{d^2x}{dt^2}=-kx$$

今回はこの定数係数二階線形同次微分方程式の解き方を解説します。

重要な事だけ知りたい方は目次からまとめにいってください。

この記事でわかることはこういったことです。

単振動とは何か
単振動の運動方程式の解き方
単振動の運動方程式の一般解

単振動とは何か？
単振動の運動方程式
まとめ

単振動とは何か？

まずはじめに単振動の運動の定義を書きます。

単振動とは、物体$m$が$x$軸上で運動しているときに、その位置が4つのパラメータ(一定値)$x_0$,$\delta$,$A$,$\omega$を用いて

$$x=x_0+A\sin(\omega t+\delta)$$

で表される運動のことです。特に$0 < \omega, \, A > 0$とします。

このときの位置の変化をグラフに示すと下図のようになります。

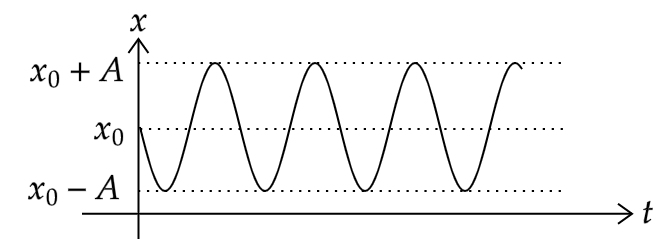
このように単振動は非常に規則的に運動します。

基本的には解くことが難しい微分方程式のなかでも単振動は解くことができます。

単振動の運動方程式

単振動を理解するためにここでは単振動が登場する運動を実際に解きます。

下のような状況を考えます。

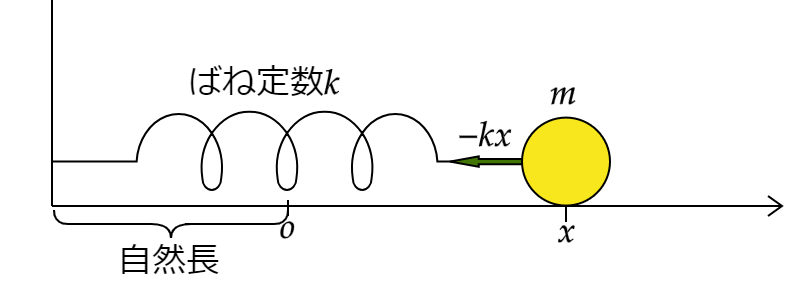
質量$m$の物体$P$がばね定数$k$のバネにつながれている。バネの自然長の場所を原点とし右向きを正ととる$x$軸を用いる。ただしバネの質量や床との摩擦、空気抵抗は無視し物体は質点として扱う。

まず運動方程式を立てます。

ばねは伸ばしたり縮めたりすると元に戻ろうとする力が働きます。このようなバネの力を弾性力といいます。その力の大きさはばね定数$k$に比例します。

運動方程式は微分方程式で、今右向きを正と取っているので、

$$m\displaystyle \frac{d^2x}{dt^2}=-kx$$

となります。これを今から解いていくことになります。

そのためにすこし微分方程式の話をします。

知ってる方はスルーしてもらって大丈夫です。

微分方程式とは

まず微分方程式とはなんでしょうか。

高校以前の数学ではこのようなものを扱ってきました。

$$x^2+7x+10=0$$

方程式を解くとは上の関係を満たす$x$(数)を見つけることでした。

ではいちばん簡単な微分方程式を例に話します。

$$\displaystyle \frac{dy}{dx}=y$$

上の微分方程式の解は何でしょうか。

これは微分方程式の知識が無くてもわかります。

つまり、微分したら自分自身になる関数とは何でしょうか。

そう指数関数です。つまり先程の微分方程式の解は

$$y=Ce^x$$

$C$は任意定数です。

このように一般に微分方程式の解は数ではなく関数になります。

微分方程式の分類について細かいことはここでは話しません。

ただ今回解こうとしている微分方程式は、「定数係数二階線形同次微分方程式」と呼ばれるタイプの微分方程式です。

単振動の微分方程式の解き方

では本題に入ります。先程の

$$m\displaystyle \frac{d^2x}{dt^2}=-kx$$

はどのように解けば良いでしょうか。

ここでは特性方程式を使用した解法を紹介します。

特性方程式

今先程の微分方程式

$$m\displaystyle \frac{d^2x}{dt^2}=-kx \tag{1}$$

の解を$\lambda$を適当に選んで$x(t)=e^{\lambda t}$　と仮定します。

そうすると$\displaystyle \frac{d^2x}{dt^2}=\lambda^2 e^{\lambda t}$になります。

$$m\displaystyle \frac{d^2x}{dt^2}=-kx$$

を次のように変形すれば、

$$\begin{align}\displaystyle \frac{d^2x}{dt^2}+\frac{k}{m}x&=\lambda^2 e^{\lambda t}+ \frac{k}{m}e^{\lambda t}\\&=\lambda^2+\frac{k}{m}=0\end{align}\tag{2}$$

となります。この式をよく見ると$\lambda$の二次方程式になっています。

つまりこの式を満たす$\lambda$を見つければ(1)の解が分かったことになります。

(2)のような式のことを特性方程式と呼びます。

ここで少し数学の解説をします。

一般に定数係数二階線形同次微分方程式には次のような性質が成り立ちます。

定数係数二階線形同次微分方程式

$$\displaystyle \frac{d^2y}{dx^2}+a\displaystyle \frac{dy}{dx}+bx=0$$

の一般解は必ず一次独立な二つの解(基本解)$y_1$,$y_2$を用いて任意定数を$C_1$,$C_2$として

$$y=C_1y_1+C_2y_2$$

の形で表すことができる。

ある微分方程式の一般解とは任意定数を含む微分方程式の解のことです。

一次独立とはこの場合、一方の解が他方の定数倍で表すことができないことをさします。

話を戻します。

さきほどの特性方程式は二次方程式でしたので解が二つ出てきます。

「解が二つ出てきて大丈夫なの」と思うかも知れませんが先程述べた通り一次独立な二つの解を定数倍して足したものが定数係数二階線形同次微分方程式の一般解となります。

では先程の特性方程式

$$\lambda^2+\frac{k}{m}=0$$

を解きましょう。二次方程式の解の公式を使えば、

$$\lambda =\displaystyle\pm \sqrt{\frac{ k }{ m }}i$$

となります。$i$は虚数単位です。$\lambda_1=\sqrt{\frac{ k }{ m }}i$,$\lambda_2=-\sqrt{\frac{ k }{ m }}i$とすると一般解は、

任意定数を$C_1$,$C_2$として

$$x(t)=C_1e^{\lambda_1 t}+C_2e^{\lambda_2 t}=C_1e^{i\omega t}+C_2e^{-i\omega t}\tag{3}$$

と書くことができます。$\omega=\displaystyle \sqrt{\frac{ k }{ m }}$です。ですが実際の物理現象などを扱うときに先程の解の実数部分だけが必要ですので、先程の解を上手く変形して実数の解を出す必要があります。

そこでオイラーの公式を使います。

オイラーの公式の使用

オイラーの公式とは

$$e^{i\theta}=\cos\theta+isin\theta$$

という式です。余談ですが、オイラーの公式は世界一美しい式だと言われたりします。特に$\theta=\pi$とすると、

$$e^{i\pi}=-1\tag{a}$$

という非常に美しい数式を導くことができます。(a)をオイラーの等式と呼んだりします。

この式は代数学において重要な虚数単位$i$,幾何学で重要な定数の円周率$\pi$,

そして解析学で重要なネイピア数$e$が一つの式でまとまっているというすごさがあります。

話を戻します。オイラーの公式をを先程の解に使うと、

$$\begin{align}(3)&=C_1(\cos(\omega t)+i\sin(\omega t))+C_2(\cos(\omega t)-i\sin(\omega t)) \\&=(C_1+C_2)\cos(\omega t)+i(C_1-C_2)\sin(\omega t)\end{align}\tag{4}$$

となります。$C_1$,$C_2$は任意定数ですので、

$$C_1=\displaystyle \frac{(B_2+iB_1)}{2}$$

$$C_2=\displaystyle \frac{(B_2-iB_1)}{2}$$

とすると$B_1$,$B_2$を用いて

$$x(t)=B_1\sin(\omega t)+B_2\cos(\omega t)\tag{5}$$

として表すことができます。$B_1$、$B_2$は任意定数(実数)です。

単振動の運動方程式の一般解

(5)でも一般解ですが、変形して先程紹介した

$$x=x_0+A\sin(\omega t+\delta)$$

にしてみましょう。ちなみに自然長を原点としているので今回導く式は$x_0=0$です。$\sqrt{B_1^2+B_2^2}=A$と置けば、

$$B_1\sin(\omega t)+B_2\cos(\omega t)\\=A\displaystyle\left\{\frac{B_1}{A}\sin(\omega t)+\frac{B_2}{A}\cos(\omega t)\right\}$$

になり、

$$\cos \delta=\frac{B_1}{\sqrt{B_1^2+B_2^2}}=\frac{B_1}{A}$$

$$\sin \delta=\frac{B_2}{\sqrt{B_1^2+B_2^2}}=\frac{B_2}{A}$$

とすると、

$$\begin{align}B_1\sin(\omega t)+B_2\cos(\omega t)&= A\{\sin(\omega t)\cos\delta\ + \cos(\omega t)\sin\delta\}\\&=A\sin(\omega t+\delta)\end{align}\tag{6}$$

となり、最初に紹介した単振動の式を導くことができました。